
Knowledge of raindrop terminal velocities from their size distributions is important in cloud physics for modeling different physical processes like breakup and coalescence, radar measurements, soil erosion studies, and hydrological applications (Doviak & Zrnic, 1993 Collier, 1996 Salles & Creutin, 2003 Montero-Martínez et al., 2009). The diurnal variation of these raindrops during different seasons is also studied.

It is observed that the superterminal raindrops are usually small in size and prolate in shape, while the subterminal raindrops are relatively large and oblate in shape. It is found that most of the superterminal raindrops occur at rain rates below 5 mm hr −1, while subterminal raindrops are relatively higher above this rain rate. Results indicate the presence of superterminal and subterminal raindrops in definite proportion in all the season with a majority of the drops have a diameter less than 1 mm. The distribution of these skewed raindrops and its relationship with rain rate, drop diameter, and axis ratio for different seasons has been examined. The ratio between the observed velocity and calculated terminal velocity is considered for estimating superterminal (positively skewed higher than terminal velocity) and subterminal (negatively skewed lower than terminal velocity) raindrops. The observed raindrop fall velocities have been corrected for the effect of air density. To increase the reliability and accuracy of analysis, the raindrops with diameters in the range 0.5–2 mm and horizontal wind speed < 2 m s −1 are considered. The analysis is for different seasons during 2012–2015.

(a) What is the coefficient of static friction? (b) What is the maximum force that can be applied upward along the plane on the rope and not move the block? (c) With a slightly greater applied force, the block will slide up the plane.Using the Two-Dimensional Video Disdrometer measurements, we investigated the fall velocity of raindrops at Mahabaleshwar (17.92°N, 73.6☎, ~1.4 km above mean sea level, AMSL), a tropical site on the Western Ghats of India. The coefficient of friction is 80% of that for the static case. In its present state, the crate is just ready to slip and start to move down the plane. A massless rope to which a force can be applied parallel to the surface is attached to the crate and leads to the top of the incline. At this point, the person’s velocity remains constant and we say that the person has reached his terminal velocity ( with the horizontal. A zero net force means that there is no acceleration, as shown by Newton’s second law. However, as the person’s velocity increases, the magnitude of the drag force increases until the magnitude of the drag force is equal to the gravitational force, thus producing a net force of zero. The downward force of gravity remains constant regardless of the velocity at which the person is moving. The two forces acting on him are the force of gravity and the drag force (ignoring the small buoyant force). For instance, consider a skydiver falling through air under the influence of gravity. Some interesting situations connected to Newton’s second law occur when considering the effects of drag forces upon a moving object. One consequence is that careful and precise guidelines must be continuously developed to maintain the integrity of the sport. Such innovations can have the effect of slicing away milliseconds in a race, sometimes making the difference between a gold and a silver medal. Most elite swimmers (and cyclists) shave their body hair. Many swimmers in the 2008 Beijing Olympics wore (Speedo) body suits it might have made a difference in breaking many world records ( (Figure)).
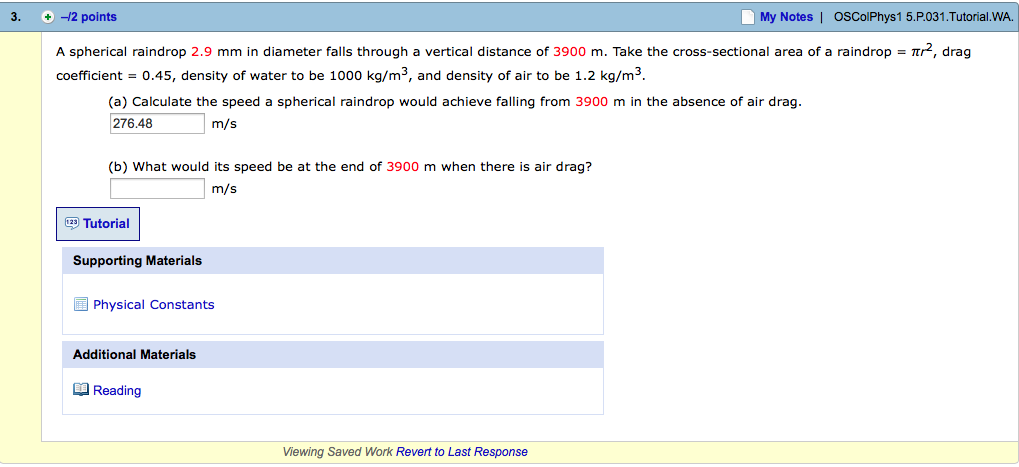
Calculate the velocity of a spherical raindrop full#
Australian Cathy Freeman wore a full body suit in the 2000 Sydney Olympics and won a gold medal in the 400-m race. Bicycle racers and some swimmers and runners wear full bodysuits. The dimples on golf balls are being redesigned, as are the clothes that athletes wear. Substantial research is under way in the sporting world to minimize drag. Typical Values of Drag Coefficient C Object For this reason, during the 1970s oil crisis in the United States, maximum speeds on highways were set at about 90 km/h (55 mi/h).

The most fuel-efficient cruising speed is about 70–80 km/h (about 45–50 mi/h). At highway speeds, over 50% of the power of a car is used to overcome air drag. Notice that the drag coefficient is a dimensionless quantity. (Figure) lists some typical drag coefficients for a variety of objects. The drag coefficient can depend upon velocity, but we assume that it is a constant here.


 0 kommentar(er)
0 kommentar(er)
